What is the Continuity Correction Factor?
Continuity correction factor
Because the normal distribution can take all real numbers (is continuous) but the binomial distribution can only take integer values (is discrete), a normal approximation to the binomial should identify the binonial event "8" with the normal interval "(7.5, 8.5)" (and similarly for other integer values). The figure below shows that for P(X > 7) we want the magenta region which starts at 7.5.
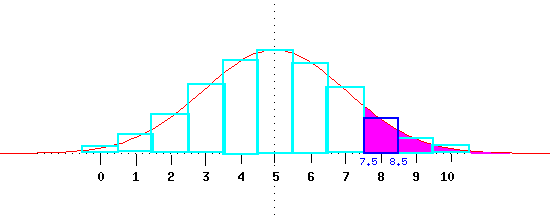
Example: If n=20 and p=.25, what is the probability that X is greater than or equal to 8?
- The normal approximation without the continuity correction factor yields
z=(8-20 × .25)/(20 × .25 × .75)^.5 = 1.55, hence P(X *greater than or equal to* 8) is approximately .0606 (from the table). - The continuity correction factor requires us to use 7.5 in order to include 8 since the inequality is weak and we want the region to the right. z = (7.5 - 5)/(20 × .25 × .75)^.5 = 1.29, hence the area under the normal curve (magenta in the figure above) is .0985.
- The exact solution is .1019 approximation
Competencies: Use the normal approximation with the continuity correction factor to approximate the probability of more than 40 successes if n=60 and p=.75.
A continuity correction factor is used when you use a continuous function to approximate a discrete one. For example, when you want to approximate a binomial with a normal distribution. According to the Central Limit Theorem, the sample mean of a distribution becomes approximately normal if the sample size is large enough. Thebinomial distribution can be approximated with a normal distribution too, as long as n*p and n*q are both at least 5.
Continuity Correction Factor Table
If P(X=n) use P(n – 0.5 < X < n + 0.5)
If P(X>n) use P(X > n + 0.5)
If P(X≤n) use P(X < n + 0.5)
If P (X<n) use P(X < n – 0.5)
If P(X ≥ n) use P(X > n – 0.5)
If P(X>n) use P(X > n + 0.5)
If P(X≤n) use P(X < n + 0.5)
If P (X<n) use P(X < n – 0.5)
If P(X ≥ n) use P(X > n – 0.5)
A numerical example: Toss a fair coin times. Approximate the probability that the number of heads is .
By working directly with the binomial, and software, I get this is, to figures, . That's the "right" answer.
Using , where is normal mean , standard deviation , no continuity correction, I get the approximation .
Using the continuity correction, I get the approximation . I should really do a few other examples, the continuity correction is too good here!
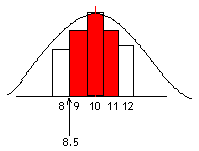
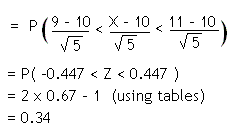
In this diagram, the rectangles represent the binomial distribution and the curve is the normal distribution:
We want P(9 ≤ X ≤ 11), which is the red shaded area. Notice that the first rectangle starts at 8.5 and the last rectangle ends at 11.5 . Using a continuity correction, therefore, our probability becomes P(8.5 < X < 11.5) in the normal distribution.
Standardising
No comments:
Post a Comment